[알고리즘] 외판원 문제 (TSP; Traveling Sales-man Problem)

외판원 문제란?

외판원이 n개 도시로 판매출장을 계획하고 있다고 가정하고, 각 도시마다 다른 도시로 이어지는 도로가 연결되어 있다. 출장시간을 최소로 줄이기 위해 외판원이 거주하고 있는 도시에서 출발하여 각 도시를 한번씩 방문하고, 다시 출발한 도시로 돌아오는 가장 짧은 여행길을 찾는 문제이다.

이 문제는 마디(Vertex, node)를 도시로 하여 가중치 포함 그래프로 표현할 수 있다.(가중치는 양의 정수로 가정)

방향 그래프에서 일주여행길은 한 도시에서 출발하여 다른 모든 도시를 한번씩만 들리고 출발한 도시로 돌아오는 여행길이다. (이를 헤밀톤 회로 라고도 한다.)

외판원 문제는 최소한 하나의 일주여행길이 존재하는 경우 가중치 포함 방향그래프에서 최적일주여행길을 찾는 문제이다.

출발도시가 어디 부터인지는 최적일주여행길을 찾는지와는 관계가 없다. 왜?

출처: https://suhyeokeee.tistory.com/115

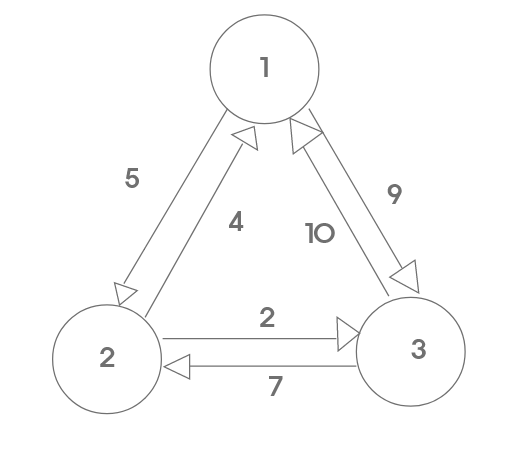
좋은 그림이 있어 가져왔다.

1부터 출발할때:  min((9+7+4), (5+2+10)) = 17

2부터 출발할때: min((4+9+7), (2+10+5)) = 17

3부터 출발할때: min((7+4+9), (10+5+2)) = 17

보이듯이 최단경로의 사이클은 모두 같은 경로만을 사용하고 있다. 5, 2, 10의 도로를 사용하지만 순서만 바뀌는 중인것을 볼 수 있다. 

따라서 출발점은 아무곳인 1이라 가정하고 1 -> 2 -> 3 -> 1 로 탐색한 값과 1-> 3 -> 2 -> 1로 탐색한 값중 최소의 값을 갖는 경로가 정답이 될 것이다.

---

완전탐색으로 풀기

접근 방법은 간단하다. 각 도시를 잇는 모든 경로를 만들고 그 중 최소값을 갖는 경로를 택한다.

완전탐색의 시간복잡도는? 크기가 모두 다른 n개의 도시를 줄세우는 경우의 수와 같다. O(N!)

n이 조금만 커져도 엄청나게 느려진다. (n=16이라면 16!은 14자리수로 10조가 넘음)

그만 알아보도록 하자.

동적계획법(DP)으로 풀기

그림

이 그림의 최적 경로는 [$v_1, v_3, v_4, v_2, v_1$] 이다.   (9 + 8 + 3 + 1 = 21)

시작을 $v_1$이라 가정한다.
$v_k$가 최적의 경로상에서 $v_1$ 다음에 오는 첫번째 도시라면, $v_k$에서 $v_1$로 가는 일주여행길의 부분 경로는 다른 도시를 정확히 한 번씩만 거치며 $v_k$에서 $v_1$으로 가는 최단경로이어야 한다. 이 말은 최적의 원칙이 성립하고 동적계획을 적용할 수 있음을 의미한다. 위 그림의 그래프를 인접행렬로 표현해보자.

인접행렬 W

V = 모든 도시의 집합

A = V의 부분집합

D[$v_i$][A] = V에 속한 도시를 각각 한 번씩만 거쳐서 $v_i$ 에서 $v_1$로 가는 최단경로의 길이

• A가 공집합인 경우 ($v_1$에서 다른 한 도시만 방문하는 경우를 말한다.)
  
  • $D[v_2][\phi] = 1   (v_2 \rightarrow v_1)$  
  • $D[v_3][\phi] = \infty   (v_3 \rightarrow v_1)$
  • $D[v_4][\phi] = 6   (v_4 \rightarrow v_1)$
• A원소가 1개 있을 때
  • $D[v_2][{v_3}] = 6 + \infty = \infty (v_2 \rightarrow v_3 \rightarrow v_1) $
  • $D[v_2][{v_4}] = 4 + 6 = 10 (v_2 \rightarrow v_4 \rightarrow v_1)$
  • $D[v_3][{v_2}] = 7 + 1 = 8 (v_3 \rightarrow v_2 \rightarrow v_1) $
  • $D[v_3][{v_4}] = 8 + 6 = 14 (v_3 \rightarrow v_4 \rightarrow v_1) $
  • $D[v_4][{v_2}] = 3 + 1 = 4 (v_4 \rightarrow v_2 \rightarrow v_1) $
  • $D[v_4][{v_3}] = \infty + \infty = \infty (v_4 \rightarrow v_3 \rightarrow v_1) $

앞에서 계산 해둔 값이 재사용 되는 것을 확인할 수 있다.

의사코드 (pseudo code)

void travel(int n, const number W[], index P[][], number& minlength) {
  index i, j, k;
  number D[1..n][subset of V-{v1}];
  
  for(i=2; i<=n; i++)
    D[i][∅] = W[i][1];
    
    for(k=1; k<= n-2; k++)
      for(A ⊆ V-{v1} 를 만족하며 마디가 k개인 모든 부분집합 A)
        for(i ≠ 1 과 , vi !∈ A 를 만족하는 모든 i) {
          D[i][A] = min(W[i][j] + D[j][A-{vj}]); 	//(j:vj∈A) //basic operation
          P[i][A] = 최소가 되는 j 값;
        }
     
      D[1][V-{v1}] = min(W[1][j]+D[j][V-{v1,vj}]);		//2<=j<=n)
      P[1][V-{v1}] = 최소가 되는 j 값;
      minlength = D[1][V-{v1}]
}

평균 시간복잡도 Θ($n^2 2^n $)